Sampling & Sampling Distribution Series # 4

 

                        

                              Sampling & Sampling Distribution

 Sampling Distribution of Sample Mean: 

The Sampling Distribution of the Sample Mean. If repeated random samples of a given size n are taken from a population of values for a quantitative variable, where the population mean is μ (mu) and the population standard deviation is σ (sigma) then the mean of all sample means (x-bars) is population mean μ (mu).

Why is sampling distribution of the mean important?

The sampling distribution of the sample mean is very useful because it can tell us the probability of getting any specific mean from a random sample. ... Standard Error of the Mean One aspect we often use from the sampling distribution in inferential statistics is the standard error of the mean (noted as SE, or SEM).

What is the mean of the sampling distribution of the sample mean quizlet?

Sampling Error is the error resulting from using a sample to estimate a population characteristic. ... The Sampling Distribution of the Sample Mean is the distribution of all possible sample means of a given sample size. You just studied 14 terms!

What is the sample mean symbol? 

x̄

The sample mean symbol is x̄, pronounced “x bar”.

Is sampling distribution always normal?

In other words, regardless of whether the population distribution is normal, the sampling distribution of the sample mean will always be normal, which is profound! ... The central limit theorem (CLT) is a theorem that gives us a way to turn a non-normal distribution into a normal distribution. 

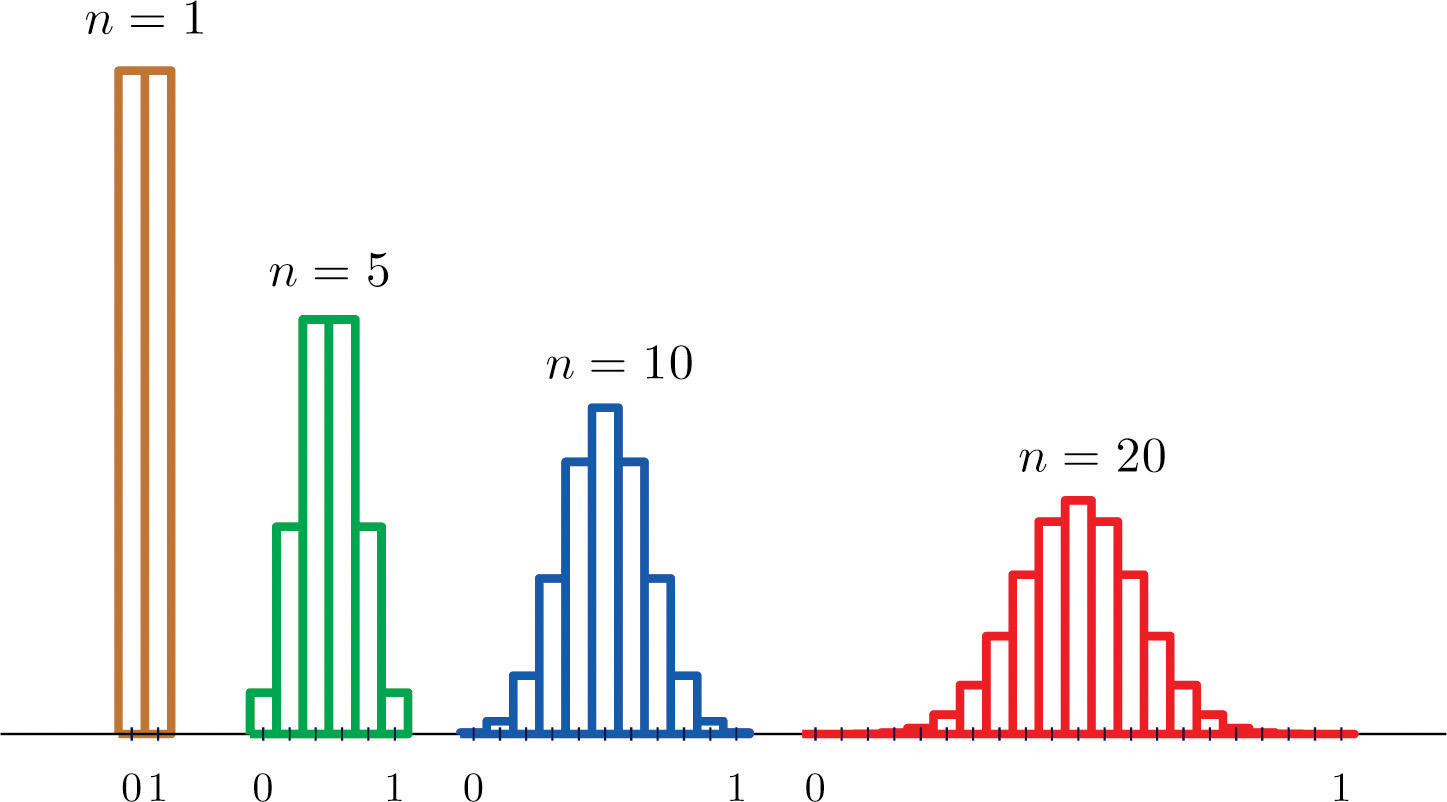
Figure 6.1 Distributions of the Sample Mean

 

As n increases the sampling distribution of X−−$\stackrel{-}{\mathit{X}}$ evolves in an interesting way: the probabilities on the lower and the upper ends shrink and the probabilities in the middle become larger in relation to them. If we were to continue to increase n then the shape of the sampling distribution would become smoother and more bell-shaped.

What we are seeing in these examples does not depend on the particular population distributions involved. In general, one may start with any distribution and the sampling distribution of the sample mean will increasingly resemble the bell-shaped normal curve as the sample size increases. This is the content of the Central Limit Theorem.

Figure 6.3 Distribution of Populations and Sample Means

The dashed vertical lines in the figures locate the population mean. Regardless of the distribution of the population, as the sample size is increased the shape of the sampling distribution of the sample mean becomes increasingly bell-shaped, centered on the population mean. Typically by the time the sample size is 30 the distribution of the sample mean is practically the same as a normal distribution.

The importance of the Central Limit Theorem is that it allows us to make probability statements about the sample mean, specifically in relation to its value in comparison to the population mean, as we will see in the examples. But to use the result properly we must first realize that there are two separate random variables (and therefore two probability distributions) at play:

1. X, the measurement of a single element selected at random from the population; the distribution of X is the distribution of the population, with mean the population mean μ and standard deviation the population standard deviation σ;
2. X−−$\stackrel{-}{\mathit{X}}$, the mean of the measurements in a sample of size n; the distribution of X−−$\stackrel{-}{\mathit{X}}$ is its sampling distribution, with mean μX−−=μ${\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}=\mathit{\mu }$ and standard deviation σX−−=σ/n−−√.

EXAMPLE 3

Let X−−$\stackrel{-}{\mathit{X}}$ be the mean of a random sample of size 50 drawn from a population with mean 112 and standard deviation 40.

1. Find the mean and standard deviation of X−−.$\stackrel{-}{\mathit{X}}.$
2. Find the probability that X−−$\stackrel{-}{\mathit{X}}$ assumes a value between 110 and 114.
3. Find the probability that X−−$\stackrel{-}{\mathit{X}}$ assumes a value greater than 113.

Solution

1. By the formulas in the previous section

   μX−−=μ=112 and σX−−=σn−−√=4050−−√=5.65685$${\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}=\mathit{\mu }=112\text{and}{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}=\frac{\mathit{\sigma }}{\sqrt{n}}=\frac{40}{\sqrt{50}}=5.65685$$

2. Since the sample size is at least 30, the Central Limit Theorem applies: X−−$\stackrel{-}{\mathit{X}}$ is approximately normally distributed. We compute probabilities using Figure 12.2 "Cumulative Normal Probability" in the usual way, just being careful to use σX−−${\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}$ and not σ when we standardize:

   P(110<X−−<114)=P(110−μX−−σX−−<Z<114−μX−−σX−−)=P(110−1125.65685<Z<114−1125.65685)=P(−0.35<Z<0.35)=0.6368−0.3632=0.2736$$\begin{array}{ll}P(110<\stackrel{-}{\mathit{X}}<114)\hfill & =P\left(\frac{110-{\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}}{{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}}<Z<\frac{114-{\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}}{{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}}\right)\hfill \\ \hfill & =P\left(\frac{110-112}{5.65685}<Z<\frac{114-112}{5.65685}\right)\hfill \\ \hfill & =P\left(\text{−}0.35<Z<0.35\right)=0.6368-0.3632=0.2736\hfill \end{array}$$

3. Similarly

   P(X−−>113)=P(Z>113−μX−−σX−−)=P(Z>113−1125.65685)=P(Z>0.18)=1−P(Z<0.18)=1−0.5714=0.4286$$\begin{array}{ll}P(\stackrel{-}{\mathit{X}}>113)\hfill & =P\left(Z>\frac{113-{\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}}{{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}}\right)\hfill \\ \hfill & =P\left(Z>\frac{113-112}{5.65685}\right)\hfill \\ \hfill & =P\left(Z>0.18\right)\hfill \\ \hfill & =1-P(Z<0.18)=1-0.5714=0.4286\hfill \end{array}$$

EXAMPLE 3

Let X−−$\stackrel{-}{\mathit{X}}$ be the mean of a random sample of size 50 drawn from a population with mean 112 and standard deviation 40.

1. Find the mean and standard deviation of X−−.$\stackrel{-}{\mathit{X}}.$
2. Find the probability that X−−$\stackrel{-}{\mathit{X}}$ assumes a value between 110 and 114.
3. Find the probability that X−−$\stackrel{-}{\mathit{X}}$ assumes a value greater than 113.

Solution

1. By the formulas in the previous section

   μX−−=μ=112 and σX−−=σn−−√=4050−−√=5.65685$${\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}=\mathit{\mu }=112\text{and}{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}=\frac{\mathit{\sigma }}{\sqrt{n}}=\frac{40}{\sqrt{50}}=5.65685$$

2. Since the sample size is at least 30, the Central Limit Theorem applies: X−−$\stackrel{-}{\mathit{X}}$ is approximately normally distributed. We compute probabilities using Figure 12.2 "Cumulative Normal Probability" in the usual way, just being careful to use σX−−${\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}$ and not σ when we standardize:

   P(110<X−−<114)=P(110−μX−−σX−−<Z<114−μX−−σX−−)=P(110−1125.65685<Z<114−1125.65685)=P(−0.35<Z<0.35)=0.6368−0.3632=0.2736$$\begin{array}{ll}P(110<\stackrel{-}{\mathit{X}}<114)\hfill & =P\left(\frac{110-{\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}}{{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}}<Z<\frac{114-{\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}}{{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}}\right)\hfill \\ \hfill & =P\left(\frac{110-112}{5.65685}<Z<\frac{114-112}{5.65685}\right)\hfill \\ \hfill & =P\left(\text{−}0.35<Z<0.35\right)=0.6368-0.3632=0.2736\hfill \end{array}$$

3. Similarly

   P(X−−>113)=P(Z>113−μX−−σX−−)=P(Z>113−1125.65685)=P(Z>0.18)=1−P(Z<0.18)=1−0.5714=0.4286$$\begin{array}{ll}P(\stackrel{-}{\mathit{X}}>113)\hfill & =P\left(Z>\frac{113-{\mathit{\mu }}_{\stackrel{-}{\mathit{X}}}}{{\mathit{\sigma }}_{\stackrel{-}{\mathit{X}}}}\right)\hfill \\ \hfill & =P\left(Z>\frac{113-112}{5.65685}\right)\hfill \\ \hfill & =P\left(Z>0.18\right)\hfill \\ \hfill & =1-P(Z<0.18)=1-0.5714=0.4286\hfill \end{array}$$

Note that if in Note 6.11 "Example 3" we had been asked to compute the probability that the value of a single randomly selected element of the population exceeds 113, that is, to compute the number P(X > 113), we would not have been able to do so, since we do not know the distribution of X, but only that its mean is 112 and its standard deviation is 40. By contrast we could compute P(X−−>113)$P\left(\stackrel{-}{\mathit{X}}>113\right)$ even without complete knowledge of the distribution of X because the Central Limit Theorem guarantees that X−−$\stackrel{-}{\mathit{X}}$ is approximately normal.

EXAMPLE 4

The numerical population of grade point averages at a college has mean 2.61 and standard deviation 0.5. If a random sample of size 100 is taken from the population, what is the probability that the sample mean will be between 2.51 and 2.71?

HOPEFULLY THIS BLOG HELPFULL FORV YOU...THANKS FOR VIEWING MY BLOG...SPORTING  ME...WE WILL MET IN THE NEXT BLOG...THANKS

https://statistics89110.blogspot.com/



Preview





Publish





Preview





Publish